Have you ever wanted to build your own calculator, query language, or even web browser? Parsers and Transformers are tremendously useful for these applications and many more, and thanks to tools like Salsify's own Botanist you don't need to be an expert in compiler design to work with them.
Many applications of parsers and transformers are in interpreters and compilers for programming languages. In fact, At Salsify we use parsers and transformers to interpret our set-based product filtering DSL (Domain Specific Language). This language encodes complex search queries such as “Find all size 10 or 11 sneakers with white soles” in structured filter strings. Botanist allows us to interpret those strings to build a user interface that enables editing those queries. Rather than get too deep into Salsify’s domain model and use case I’ll walk you through a simple example where transformers come in handy.
Starting Small
Botanist is a library for generating tree transforms. Its role is to make it easier to work with deeply-nested objects, but I see it as a powerful tool for interpreting and reshaping data. For example, here is how an arithmetic evaluator might compute the result of the expression (5 + 9) * (6 - 3). The parser generates a tree by creating a node for each operation and value such that the nodes to be evaluated earlier are closer to being leaves. In other words, the tree represents the expression in such a way that we can evaluate it from the bottom up.
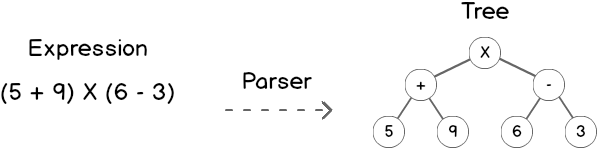
There are more in-depth explanations for how to parse an expression and generate this type of tree, but let’s focus on the transformation aspect of this expression evaluator. We compute the value of the expression this tree represents by defining rules to be applied to its subtrees. Botanist’s rules provides a declarative way of specifying operations to apply to parts of a tree. A rule in Botanist consists of a matcher for a subtree and a function to be applied to that subtree. Here we might specify a rule for each type of arithmetic operation and its values. When we apply our transform to the tree, Botanist runs through each node, starting with the leaves, and applies the matching rule to modify it. At each operation node we return the result of applying the operation to its children. For example, at the “minus” operation we subtract 3 from 6 and return 3, replacing that “minus” operation with this value. Once we’ve finished transforming the tree we are left with the result of the expression. A potential implementation of this evaluator can be seen on the Botanist github page. The value of transformers, like the ones Botanist generates, is to reshape data. In this case, we’re transforming a tree representing a mathematical expression into the value of that expression. And that’s just where the fun begins.
Apples to Applications
Suppose we want to build a web application to display man pages in a more user friendly way. It might have a navigable table of contents, collapsible sections, and links to other man pages or websites. We can approach the design of this application by parsing man pages and transforming them to create the data and UI elements that the user will be interacting with. The parser would be responsible for generating a tree representing the structure of the document. From there we can use a transform created with Botanist to decorate parts of the tree and map its structure directly to the structure of our application. Here's a rough sketch of how we go from man page to web app.
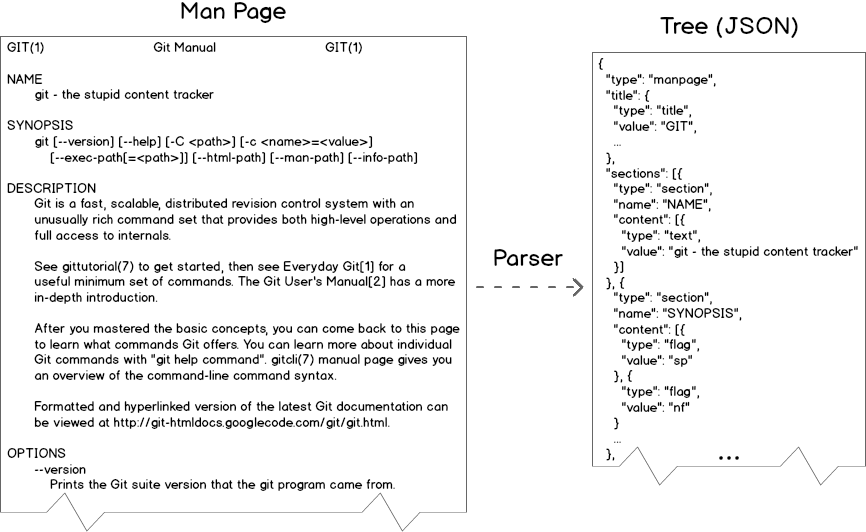
The first step involves parsing the man page to create a tree. We'll use the troff format version of the document, which you can view yourself using cat $(man -w git). This document contains text and some troff-specific commands to format the text. Its use of special tags makes it straightforward to parse this document and recognize structural elements such as sections, links, and titles. I won’t show the parser here, but we could use a tool like PEG.js to generate a parser for documents like this. As you can see in the sample tree, we've got a few types of objects including manpages, titles, and sections. This structure brings us a bit closer to data that is usable in an application.
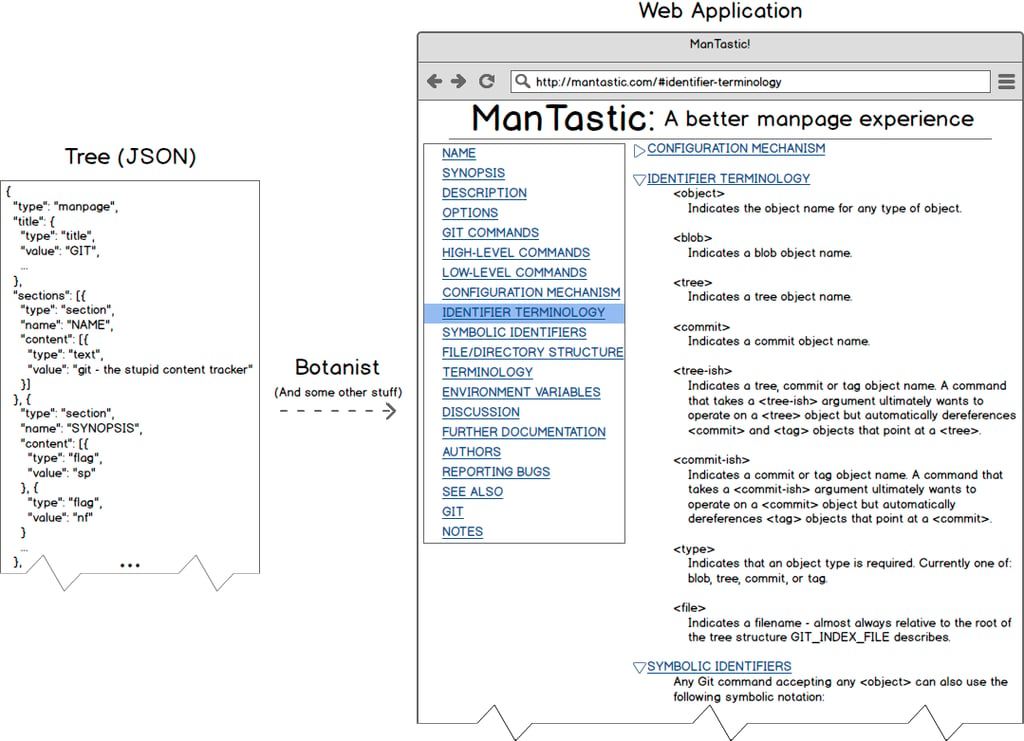
The next step is where Botanist comes in, taking our tree and turning it into something resembling a full application. As mentioned in the arithmetic evaluator example, Botanist relies on rules to transform trees. Each rule consists of matching criteria and an operation to be performed on matched nodes. For example, the following transform, consisting of a single rule, would turn any url object in the tree into an html anchor tag. We match this rule based on string comparison of the type property and use the simple matcher on the value, meaning it can be any Javascript primitive. This might be valuable for the most simple use-case, transforming a man page into static html.
The real value of the transforms Botanist creates comes from its ability to recursively apply these rules to any node in the tree. Just adding the following two rules will enable us to build a full webpage of arbitrarily nested sections, populated with text and links.
Botanist applies rules to your tree from the bottom up. This means when that top level section is evaluated, everything in its content array has been transformed into strings and we can use them to build our document. The other key takeaway is the introduction of the subtree matcher. It allows us to match any value, in this case we want to match the array of content strings. There are more details about available matchers in the Botanist docs. Essentially what we're doing in this example is transforming one tree into another tree-like structure, an HTML document.
Getting back to our man page application use case, I suggested we could use Botanist to turn a basic tree data structure into a web app. This may seem like an oversimplification, but the JSON tree our parser creates is already a simple analog of the tree of views and components of a web application. With properly defined application components, Botanist can simply match subtrees and transform them until your full application hierarchy has been constructed. The following is a potential implementation of a Section class to render and manage state for sections of our man page. Following this pattern and defining rules and views for every node type in our tree completes our journey from simple text document to rich web app.
Now we're thinking with trees
I hope this whets your appetite to try building your own parsers and transformers. They are appropriate not only for the common use cases of compilers and interpreters, but for a host of common problems we face as developers. Most of all, they are less error prone and easier to alter or extend than hand-built parsers. Sometimes all you need to do to make data useful is turn it into a tree and decorate it.
Further Reading

